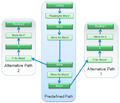
Hierarchical structure (levels)
|
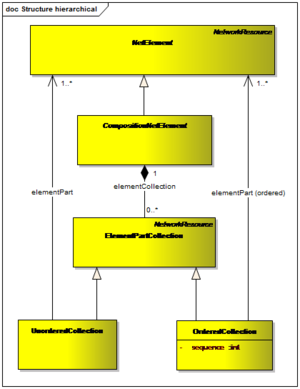
To describe the hierarchical structure of a “Network” instance which is built from “NetElement” instances belonging to different description levels the RailTopoModel® provides the classes “CompositionNetElement”, “ElementPartCollection”, “OrderedCollection” and “UnorderedCollection”.
The important difference between “OrderedCollection” and “UnorderedCollection” is the possibility to enforce a sequence in the “NetElements” children at the more detailed description level.
The fact that a given “NetElement” instance is composed from “NetElement” instances of a more detailed description level is modelled with the “CompositionNetElement” class.
Aggregation
The following step-by-step example shows the principle of aggregation.
Starting point is a sample railway network at micro level depicting switches and tracks.
The aggregation shall produce "OperatingPoints" (OP) on an aggregated level out of the micro level to be used in more generalised applications:
Following the RailTopoModel® principes, the original network is modelled this way (each dot represents a NetElement):
The target OPs have known boundaries that happen to be situated somewhere on the tracks. In reality, these boundaries are for example given by the station signals. So, the tracks containing those boundaries have to be split into parts in order to identify what falls inside the boundaries and what stays outside.
The RailTopoModel® provides structures to split the "NetElement" instances. For each "NetElement" instance that has to be broken up, two (or more) "LinearElementPart" instances are created. The first part runs from 0 to the split point, the other part runs from the split point to 1 (or to the next split point), effectively forming two (or more) new elements on another level.
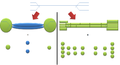
The resulting network will be depicted as follows (Each dot is an "ElementPart", those in orange are the new "ElementParts" resulting from a split, those in blue and green are "ElementParts" that keep the totality of their parent element):
At this step, the advantage of considering linear and non-linear elements in the same way of modelling can be seen: The graph theory provides tools to aggregate nodes of a graph. All "NetElements" are seen as nodes and can be easily aggregated to form a new network:
Using the previously introduced symbology (where the blue dots represent linear elements and green dots represent nonlinear elements) the green rectangles show indicate how the elements will be aggregated to obtain the target description of the network:
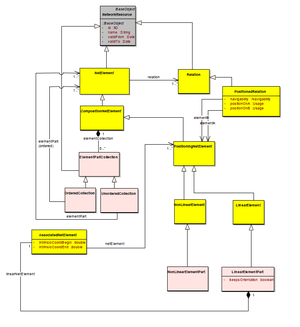
Structure Model
In order to being able to model the aggregation as described in this section, the RailTopoModel® contains a number of classes as can be seen in the figure.
Ordered and unordered collections
The "OrderedCollection" defines a collection that has to be a continuous string of elements, without orientation changes. By using an "OrderedCollection" it is possible to compute a length and orientation. Let's have a look at a sample railway network:
The red collection of track segments shown in the next picture is an "OrderedCollection": it has a start, an end and it is possible to compute a length.
The "UnorderedCollection" is more generic. Like in an "OrderedCollection" still all elements are connected, but it is not possible to calulate a length or derive an orientation. In the following figure, the purple collection is an "UnorderedCollection"
An "UnorderedCollection" may have more than one start, more than one end and different lengths.
Disaggregation
This section proposes a modelling concept for disaggregation, which is compliant with the RailTopoModel®. In most cases that the different hierarchical levels of the topology network are derived via aggregation from nano level to macro level, but it is also possible to follow the other way from an aggregated level to a more detailed one. However, this concept of disaggregation requires additional information or at least "modelling templates" for disaggregating the nodes. Examples for such "modelling templates" are a default station layout, a standard switch layout, etc.
The procedure of disaggregation seems to be very useful as a system function for capacity planning or for the fast configuration of simulation datasets in situations of inadequate or outdated base documentation.
The orientation of the Part needs not be the same as the orientation of the parent. The parameter KeepsOrientation allows to reverse the element in order to keep a homogeneous orientation for the collection.
In the following example we assume that the starting point is the macro level of detail for the network, and that we want to produce a more detailed level:
In the model view this railway network is translated into:
For disaggregation of this OP, we assume the following template of a standard station layout:
The resulting object model is depicted in the following figure:
Afterwards, the adjacent linear elements (blue dots) are fused if required.
The resulting railway network model is depicted in the following figure:
To summarize:
Aggregation/Disaggregation are done in two steps: at first the elements are decomposed into "element parts" and then the parts are fused together to create new elements. There is thus very little difference between aggregation and disaggregation, the main difference is the purpose of the operation. While aggregation simplifies the network and reduces the number of elements, disaggregation raises this number by adding detail to the network.
Different Level Views
As show in the previous section, there are two ways of applying aggregation/disaggregation procedures:
Depending on how the created level will be linked to the existing level, the procedure might produce a higher or a lower description level of detail.
- A lower level is produced when information is added to the original Elements level.
- A higher level is produced if the objects of the new level can be derived as a function of the objects of the original level.
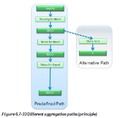
Higher level view
Disaggregation of a higher level amounts to creating an alternative path. In other words creating another "Branch" in the tree of level definitions. For example, one may want to divide the network following a station/open track rule - the "predefined path" - for path calculation purposes, and divide it into track circuits for train tracking and control.
The track circuits have to be defined as collection of parts of the elements of the base network.
Fortunately, the RailTopoModel® allows an infinite number of those branches.
In the previous example, the function of macro level could be defined both in terms of the Station/open track definition and as a collection of track circuits.
Both path give a valid network (in that sense that the network obeys the model’s rules), but the two results may not always be identical.
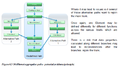
Lower level view
Building downwards, in fact multiple "roots" are created from the trunk, adding a new definition of the elements to the "base" level. It is important to be careful and ensure that the multiple definitions result in exactly the same element at the base level.
It also means that, an element at any level may have several definitions, depending on what level is considered as the source, and that a routing level has to be built at the end of each “root”. As the roots never rejoin the trunk (else, they would be built upwards) there is no real issue concerning the data coherency. As long as the client is conscious from which root he takes the data.
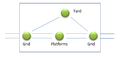
For example, a station may have several definitions, whether viewed from the point of a signalman, a passenger operator.
In the signalman’s view, all the tracks and switches are important. In the operator’s view, the platforms and the yard are the main elements in this view. The two definitions may be considered equivalent if there is an agreement of the boundaries, meaning that what is inside and outside stays the same(geographically or functionally).
What you should have learned
|
| What you should have learned | |||
|---|---|---|---|
| |||
| Navigation | |||
| Home | ← | • | → |
| Chapter | RailTopoModel® Quick Start | RailTopoModel® Modelling Concepts | RailTopoModel® External References |
| Section | Levels of detail | structure | Positioning |
| Subection | Topological structure (network) | Hierarchical structure (levels) | |