Positioning: Difference between revisions
| [checked revision] | [checked revision] |
Ferri Leberl (talk | contribs) (Änderung Navi) |
Ferri Leberl (talk | contribs) m (→Coordinate positioning: {{main}}) |
||
| Line 1: | Line 1: | ||
== Coordinate positioning == | == Coordinate positioning == | ||
{{main|Coordinate positioning}} | |||
== Linear Positioning / referencing == | == Linear Positioning / referencing == | ||
Linear Referencing Systems (LRS) are widely used in the transportation world. They allow specifying positions along linear elements by using distances measured along the element (possibly with a lateral and horizontal offset), not by using classical 2D or 3D coordinating systems (CRS). <br /> | Linear Referencing Systems (LRS) are widely used in the transportation world. They allow specifying positions along linear elements by using distances measured along the element (possibly with a lateral and horizontal offset), not by using classical 2D or 3D coordinating systems (CRS). <br /> | ||
Revision as of 16:55, 13 March 2017
Coordinate positioning
- →Main Article: Coordinate positioning
Linear Positioning / referencing
Linear Referencing Systems (LRS) are widely used in the transportation world. They allow specifying positions along linear elements by using distances measured along the element (possibly with a lateral and horizontal offset), not by using classical 2D or 3D coordinating systems (CRS).
Locating an object with linear coordinates makes sense for various reasons. First of all, a large amount of information is stored in databases from legacy systems, anterior to geographical information systems which are specifically designed to deal with classical CRS. Knowing where an object is located along a route or a pipeline is sufficient to use the data from those databases, and can be seen as an integration mean for data coming from different sources.
It is even sometimes more interesting to have a linear position than a spatial position. Knowing that you have train stopped at about the kilometre 45 on the Line 36 Track A is better than having a potentially more accurate GPS position, which does neither tell without ambiguity on which line nor track it stands.
Norms
Linear Referencing is the object of the European Norm EN19148:2012.
The RailTopoModel® follows the same principles, but uses a simplified version of the model as a lot of cases foreseen in the norm are not encountered in the railways world.
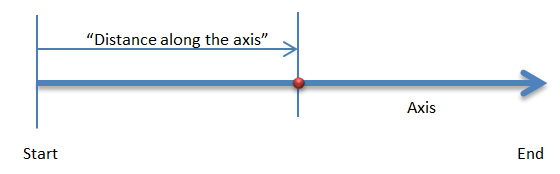
Axis
A linear referencing system has an axis along which the measures are done. The axis can be any linear entity, a track segment or a whole line. It does not need to have geometry as knowing its length is enough to use an LRS.
Referencing Methods
A Linear Referencing System may use several methods to describe a position along an axis:
- Absolute : the position is specified by giving the distance starting at the beginning of the axis (with an eventual offset)
Its main disadvantage is the fact that the whole length of the axis is taken into account when measuring. It means :
- that the field workers always have to begin measurement at the start of the axis. It makes it unpractical for long axes,
- that each change happening in the axis before the referenced object changes the coordinate of the measured point.
It is thus only suitable for short axes, or axes which are very stable in the scope of the measurement.
- Relative : The position is specified by giving the distance starting from an element (referent) whose position is known.
This is the most commonly used in railways, with mileposts as referents. Amongst its advantages is the stability of the coordinate which is now independent from works or axis changes happening before the referent, unless the change also affects the referent.
It is also more practical for the field workers as the measurement only has to start at the referent.
On the other hand, it forces to maintain a whole set of referents, ensuring they never move, and recalculating their position at each infrastructure change.
It makes it most suitable for long axes, such as lines, but poorly adapted to short segments (work reservations or sidings).
While it is possible to measure in both directions, (km x + y meters or km x+1 – z meters), the former method is the most widely used.
It is also the most suited to store long term information, because of the stability of the coordinates. However, it is very poorly suited to calculations as true distances are difficult to deduce from the coordinates.
Both methods can include lateral or vertical offsets.
Expression of the distance
The distance from the start of the measure (be it the start of the axis or the referent) can be expressed in several ways.
- In metres (or miles, or any unit of choice)
- Relative to the length of the element
- As a percentage of the element (0…100 %)
- Normalized (0…1). 75 % being expressed as 0.75
- Hybrid : as a percentage of the length between two successive referents
Hybrid expression
The major problem with the relative method of linear referencing is the fact that it cannot be stored as a number when the system has mileage anomalies.
As the distance between two successive referents may be more than one kilometre (or 1000 units), the coordinate needs two fields to be stored. On top of that, not all reference points have a numeric name, a referent 12A might be inserted when lengthening the track between the mileposts 12 and 13.
The hybrid method aims to deal with this issue by assigning a fixed coordinate to each successive referent (usually a multiple of 1000) and adding the percentage of the distance between the two referents.
While it doesn’t allow true distance measurement, it keeps the sequence of the objects.
For example, assuming the distance between the kilometre post 12 and 13 is 1200m and that the object needing to be located is at km 12 + 1050m,
- Kilometre post 12 : coordinate 12000
- Kilometre post 13 : coordinate 13000
Object coordinate : coordinate of the referent (12000)+ percentage of the distance of the object regarding the distance between the referents (1050/1200) multiplied by the difference of coordinates between the two successive referents (1000)
- Object coordinate : 12000 + (1050/1200)*1000 = 12875, which is a number that can be stored in one field and on which operations may be made.
RailTopoModel® structure
As the railways world uses the most suited LR method according to the case, and that the aim of RailTopoModel® is to design a universal way of describing railways, it was chosen to split the reference system into two kinds:
- The NetElement’s internal way of measuring is a normalized absolute LRS. The NetElement with its own internal LRS (which we called “Intrinsic Positioning System” as it is proper to the NetElement, created and destroyed with it) becomes a “PositioningNetElement”
- External linear referencing systems (such as the line/milepost) may be attached to the PositioningNetElement by linking a set of external LRS coordinates to the corresponding intrinsic coordinates.
Choosing a universal LRS allows designing location algorithms independently from the field situation which would decide the most practical LR method for a specific segment.
Intrinsic positioning / referencing
As said above, each NetElement forming the network has its own linear referencing system, which is created at the same time as the NetElement and destroyed with it. The purpose of this referencing system is double:
- It ensures that every NetElement has a reference system allowing to locate events on it; small track elements (e.g. work reservations or side tracks) are often not linked to any “major” linear systems such as lines)
- It ensures that every NetElement has an orientation and a length. This allows to locate other NetElements relatively to it (e.g. this switch is at the beginning of this track element)
The reason why it was decided to use a normalized absolute LRS is that the normalized expression allows designing algorithms which are disconnected from the unit system. Some distances may be expressed in kilometres, miles, centimetres or feet. The normalized notation (0…1) allows to deal separately with the unit conversions.
Also, as it is applied to the smallest element of the network (at a given level), it can be used for locating objects in any path drawn on the network topology, whatever its length or its links with external referencing systems are (path crossing two lines).
Although very difficult to interpret in human interaction, it is perfectly adapted for computer calculations.
Track-referred positioning
As the intrinsic coordinate system is difficult to use in human exchanges, field workers often use the classical linear referencing with line number, kilometre reference and distance from the post when dealing with long axis or metres from the start when dealing with short axis.
Those referencing systems can be linked with any relevant PositioningNetElement, ensuring the ability to translate the coordinates into an intrinsic coordinate and back. Any number of external reference systems can be linked to an element and an external reference system may of course be linked with several elements.
| What you should have learned | |||
|---|---|---|---|
| Please, enter a summary! | |||
| Navigation | |||
| Home | ← | • | → |
| Chapter | RailTopoModel® Quick Start | RailTopoModel® modelling concepts | RailTopoModel® External References |
| Section | Structure | Positioning | Object positioning in the network |
| Subection | |||